La Pirámide de Keops y el Teorema de Tales
La Pirámide de Keops y el Teorema de Tales
Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura.
La historia dice así:
«Un sacerdote egipcio le pregunta sonriendo cuál puede ser la altura de la pirámide del rey Khufu (la pirámide de Keops). Tales reflexiona y a continuación contesta que no se conforma con calcularla a ojo, sino que la medirá sin ayuda de ningún instrumento. Se echa sobre la arena y determina la longitud de su propio cuerpo.
Los sacerdotes le preguntan qué es lo que está pensando, y Tales les explica: «Me pondré simplemente en un extremo de esta línea, que mide la longitud de mi cuerpo, y esperaré hasta que mi sombra sea igual de larga. En ese instante , la sombra de la pirámide de vuestro Khufu también ha de medir tantos pasos como la altura de la pirámide.»
El método que utilizó Tales de Mileto para calcular la altura de la Pirámide de Keops es lo que conocemos como Teorema de Tales (parece obvio por qué se llama así).
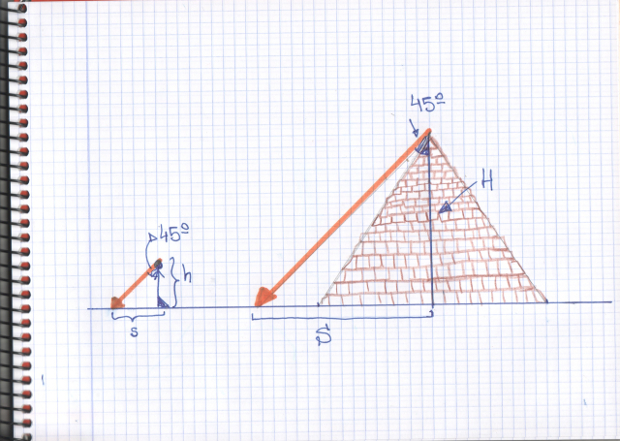
El siguiente esquema nos permite ver el problema en cuestión y cómo calculó Tales la altura de la pirámide clavando su bastón en la arena.

La sombra es la región donde no dan los rayos del sol. Se supone que los rayos que inciden en la pirámide y en el bastón son paralelos (consecuencia de la gran distancia que separa al Sol de la Tierra) y el bastón está clavado perpendicularmente al suelo.
De esta forma, los ángulos de los dos triángulos que observamos en la figura son iguales entre sí y, por tanto, dichos triángulos son semejantes.
En dos triángulos semejantes, se cumple que sus lados homólogos son proporcionales.
En nuestro caso, se cumple que:

Supongamos ahora que a una hora determinada del día, la sombra de la pirámide medía 280 metros, la sombra del bastón medía 2,87 metros y dicho bastón era de 1,5 metros. Según lo que hemos visto antes, tendríamos que:

De donde obtenemos:

Que es el valor aproximado que tenía la pirámide de Keops en la antigüedad (actualmente tiene 136,86 m).
El método que utilizó Tales de Mileto, el Teorema de Tales, tiene una enorme utilidad puesto que, entre otras muchas cosas, lo podemos emplear para averiguar la altura de cualquier objeto que sea grande sin necesidad de medirlo directamente.
–¿La pirámide de qué? –preguntó Ven con los ojos apretados.
–La gran pirámide de Guiza, una de las siete maravillas del mundo, que está en Egipto –les contó Mati.
–¡Toma! –se asombró el pequeño –¿Y cómo lo hizo , Mati?
–Pues usando su teorema –dijo la pelirroja y le guiñó un ojo –Tales pensó que cuando su sombra midiera lo mismo que él, los rayos de Sol estarían formando un ángulo de 45 grados con su cabeza y con la cima de la pirámide, y por lo tanto, la altura de la pirámide sería igual a la sombra de la misma en ese instante.
–En ese caso –continuó Mati — si llamamos h a la altura de Tales y s a la sombra del mismo, cuando s sea igual a h, los rayos de Sol forman un ángulo de 45 grados en la cabeza de Tales. Y como los rayos de Sol son paralelos unos con otros, el rayo de Sol en la cima de la pirámide también forma 45 grados y por lo tanto H es igual a S. Sólo hay que medir S para conocer H, porque estamos mirando triángulos semejantes.
–¿Cómo sabes que son semejantes, Mati? –preguntó Sal.
–Pues porque la suma de todos los ángulos internos de un triángulo es 180 grados –empezó a decir la gafotas –Como H y S forman 90 grados, igual que h y s, y el Sol forma 45 grados en la cabeza y en la cima, el ángulo que forma el Sol con el suelo en los 2 casos, tiene que ser de 45 grados; con lo cual, los tres ángulos son iguales.
–¡Toma. toma. toma! ¡Cómo mola! –Ven estaba entusiasmado.
–¿Y cómo podía Tales medir su sombra? –preguntó Sal receloso –Si se agachaba a medirla, ya no podía medirla… ¿Tenía un ayudante?
–Hay varias versiones –dijo Mati –Algunas hablan de que en realidad usó un bastón, pero hay otras que dicen que Tales pintó un círculo de radio su altura y se puso en el centro; cuando su sombra tocara el círculo, ya sabía que era tan larga como su altura.
–¡Es verdad! –Sal respiró tranquilo.
–¡Me encanta Tales! –gritó el pequeño saltando provocando que nuestro Anubis particular ladrara del susto.
–Pues no se vayan todavía, aún hay más –anunció cómicamente Mati.
–¿Qué más, Mati? –preguntó Sal intrigado.
–Pues, por ejemplo –anunció Mati –gracias a este teorema de Tales podemos dividir un segmento en el número de partes iguales que queramos. usando sólo regla y compás.
–¿¿Sí?? –preguntó el pequeño –¿¿Cómo??
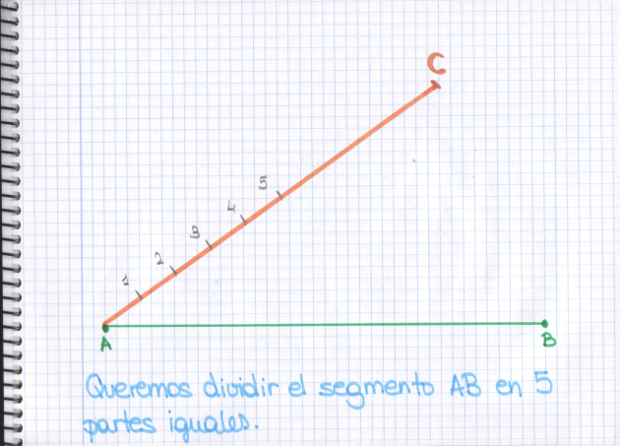
–Ya veréis –dijo la pelirroja –pintamos un segmento en nuestro cuaderno, ¿en cuántas partes iguales queréis dividirlo?
–¡En 5! –gritó Ven.
–Bien –siguió ella –ahora pintamos otro segmento formando un ángulo, el que queramos, con el segmento AB.
–¿Y ahora? –preguntó el gafotas.
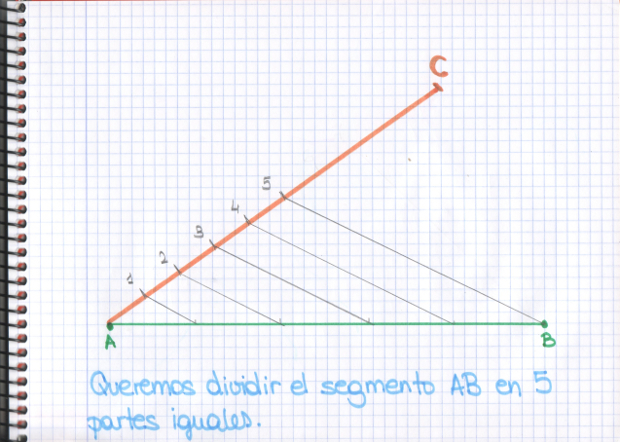
–Ahora abrimos el compás, con la medida que queráis, y marcamos 5 veces sobre el segmento AC
–Ahora sólo tenemos que unir la última marca –les dijo Mati –con el extremo B…
–…y trazar paralelas a ese segmento por las otras 4 marcas –terminó de decir Mati.
–¡Toma, toma, toma! –el pequeño Ven estaba emocionado.
–Sí que mola, Tales, sí –corroboró el gafotas.






Comentarios
Publicar un comentario